Discovering faster matrix multiplication algorithms with reinforcement learning - Nature.com

Matrix multiplication is one such primitive task, occurring in many systems—from neural networks to scientific computing routines.

However, automating the algorithm discovery procedure is intricate, as the space of possible algorithms is enormous.

Here we report a deep reinforcement learning approach based on AlphaZero1 for discovering efficient and provably correct algorithms for the multiplication of arbitrary matrices.

Our agent, AlphaTensor, is trained to play a single-player game where the objective is finding tensor decompositions within a finite factor space.

AlphaTensor discovered algorithms that outperform the state-of-the-art complexity for many matrix sizes.

We further showcase the flexibility of AlphaTensor through different use-cases: algorithms with state-of-the-art complexity for structured matrix multiplication and improved practical efficiency by optimizing matrix multiplication for runtime on specific hardware.

We focus on the fundamental task of matrix multiplication, and use deep reinforcement learning (DRL) to search for provably correct and efficient matrix multiplication algorithms.

This algorithm discovery process is particularly amenable to automation because a rich space of matrix multiplication algorithms can be formalized as low-rank decompositions of a specific three-dimensional (3D) tensor2, called the matrix multiplication tensor3,4,5,6,7.

This space of algorithms contains the standard matrix multiplication algorithm and recursive algorithms such as Strassen’s2, as well as the (unknown) asymptotically optimal algorithm.

We focus here on practical matrix multiplication algorithms, which correspond to explicit low-rank decompositions of the matrix multiplication tensor.

In contrast to two-dimensional matrices, for which efficient polynomial-time algorithms computing the rank have existed for over two centuries13, finding low-rank decompositions of 3D tensors (and beyond) is NP-hard14 and is also hard in practice.

In fact, the search space is so large that even the optimal algorithm for multiplying two 3 × 3 matrices is still unknown.

Nevertheless, in a longstanding research effort, matrix multiplication algorithms have been discovered by attacking this tensor decomposition problem using human search2,15,16, continuous optimization17,18,19 and combinatorial search20.

We instead use DRL to learn to recognize and generalize over patterns in tensors, and use the learned agent to predict efficient decompositions.

We formulate the matrix multiplication algorithm discovery procedure (that is, the tensor decomposition problem) as a single-player game, called TensorGame.

To solve TensorGame and find efficient matrix multiplication algorithms, we develop a DRL agent, AlphaTensor.

AlphaTensor is built on AlphaZero1,21, where a neural network is trained to guide a planning procedure searching for efficient matrix multiplication algorithms.

Our framework uses a single agent to decompose matrix multiplication tensors of various sizes, yielding transfer of learned decomposition techniques across various tensors.

AlphaTensor scales to a substantially larger algorithm space than what is within reach for either human or combinatorial search.

In fact, AlphaTensor discovers from scratch many provably correct matrix multiplication algorithms that improve over existing algorithms in terms of number of scalar multiplications.

AlphaTensor also discovers a diverse set of algorithms—up to thousands for each size—showing that the space of matrix multiplication algorithms is richer than previously thought.

We also exploit the diversity of discovered factorizations to improve state-of-the-art results for large matrix multiplication sizes.

Through different use-cases, we highlight AlphaTensor’s flexibility and wide applicability: AlphaTensor discovers efficient algorithms for structured matrix multiplication improving over known results, and finds efficient matrix multiplication algorithms tailored to specific hardware, by optimizing for actual runtime.

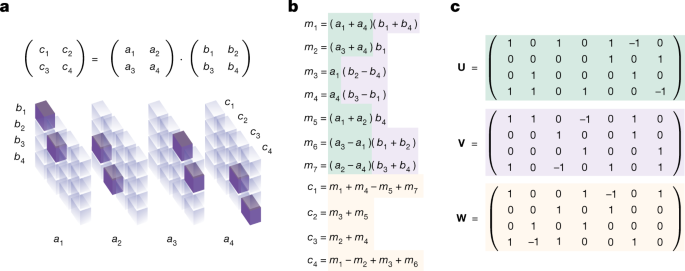
As matrix multiplication (A, B) ↦ AB is bilinear (that is, linear in both arguments), it can be fully represented by a 3D tensor: see Fig.

1a for how to represent the 2 × 2 matrix multiplication operation as a 3D tensor of size 4 × 4 × 4, and refs.

We write \({{\mathscr{T}}}_{n}\) for the tensor describing n × n matrix multiplication.

More generally, we use \({{\mathscr{T}}}_{n,m,p}\) to describe the rectangular matrix multiplication operation of size n × m with m × p (note that \({{\mathscr{T}}}_{n}={{\mathscr{T}}}_{n,n,n}\)).

If a tensor \({\mathscr{T}}\) can be decomposed into R rank-one terms, we say the rank of \({\mathscr{T}}\) is at most R, or \(\,\text{Rank}\,({\mathscr{T}}\,)\le R\).

This is a natural extension from the matrix rank, where a matrix is decomposed into \({\sum }_{r=1}^{R}{{\bf{u}}}^{(r)}\otimes {{\bf{v}}}^{(r)}\).

a, Tensor \({{\mathscr{T}}}_{2}\) representing the multiplication of two 2 × 2 matrices.

c, Strassen's algorithm in tensor factor representation.

By using this algorithm recursively, one can multiply matrices of arbitrary size, with the rank R controlling the asymptotic complexity of the algorithm.

We cast the problem of finding efficient matrix multiplication algorithms as a reinforcement learning problem, modelling the environment as a single-player game, TensorGame.

When the player reaches the zero tensor, the sequence of selected factors satisfies \({{\mathscr{T}}}_{n}={\sum }_{t=1}^{R}{{\bf{u}}}^{(t)}\otimes {{\bf{v}}}^{(t)}\otimes {{\bf{w}}}^{(t)}\) (where R denotes the number of moves), which guarantees the correctness of the resulting matrix multiplication algorithm.

If the game terminates with a non-zero tensor (after Rlimit steps), the agent receives an additional terminal reward equal to \(-\gamma ({{\mathscr{S}}}_{{R}_{\text{limit}}})\), where \(\gamma ({{\mathscr{S}}}_{{R}_{\text{limit}}})\) is an upper bound on the rank of the terminal tensor.

Although this reward optimizes for rank (and hence for the complexity of the resulting algorithm), other reward schemes can be used to optimize other properties, such as practical runtime (see ‘Algorithm discovery results’).

Besides, as our aim is to find exact matrix multiplication algorithms, we constrain {u(t), v(t), w(t)} to have entries in a user-specified discrete set of coefficients F (for example, F = {−2, −1, 0, 1, 2}).

With the above reward scheme, the distribution z models the agent’s belief about the rank of the tensor \({{\mathscr{S}}}_{t}\).

To play a game, AlphaTensor starts from the target tensor (\({{\mathscr{T}}}_{n}\)) and uses the MCTS planner at each step to choose the next action.

Overcoming the challenges posed by TensorGame—namely, an enormous action space, and game states described by large 3D tensors representing an abstract mathematical operation—requires multiple advances.

The proposed architecture, which disregards the order of rows and columns in the grids, is inspired by the invariance of the tensor rank to slice reordering.

We train the network on a mixture of supervised loss (that is, to imitate synthetic demonstrations) and standard reinforcement learning loss (that is, learning to decompose a target tensor \({{\mathscr{T}}}_{n}\)) (Fig. 2).

\({{\mathscr{T}}}_{n}\) (Fig. 1a) is the tensor representing the matrix multiplication bilinear operation in the canonical basis.

These different tensors are equivalent: they have the same rank, and decompositions obtained in a custom basis can be mapped to the canonical basis, hence obtaining a practical algorithm of the form in Algorithm 1.

We train a single AlphaTensor agent to find matrix multiplication algorithms for matrix sizes n × m with m × p, where n, m, p ≤ 5.

At the beginning of each game, we sample uniformly a triplet (n, m, p) and train AlphaTensor to decompose the  tensor \({{\mathscr{T}}}_{n,m,p}\).

Although we consider tensors of fixed size (\({{\mathscr{T}}}_{n,m,p}\) has size nm × mp × pn), the discovered algorithms can be applied recursively to multiply matrices of arbitrary size.

We use AlphaTensor to find matrix multiplication algorithms over different arithmetics—namely, modular arithmetic (that is, multiplying matrices in the quotient ring \({{\mathbb{Z}}}_{2}\)), and standard arithmetic (that is, multiplying matrices in \({\mathbb{R}}\)).

Figure 3 (left) shows the complexity (that is, rank) of the algorithms discovered by AlphaTensor.

AlphaTensor re-discovers the best algorithms known for multiplying matrices (for example, Strassen’s2 and Laderman’s15 algorithms).

More importantly, AlphaTensor improves over the best algorithms known for several matrix sizes.

In particular, AlphaTensor finds an algorithm for multiplying 4 × 4 matrices using 47 multiplications in \({{\mathbb{Z}}}_{2}\), thereby outperforming Strassen’s two-level algorithm2, which involves 72 = 49 multiplications.

By applying this algorithm recursively, one obtains a practical matrix multiplication algorithm in \({{\mathbb{Z}}}_{2}\) with complexity \({\mathcal{O}}({N}^{2.778})\).

‘Best rank known’ refers to the best known upper bound on the tensor rank (before this paper), whereas ‘AlphaTensor rank’ reports the rank upper bounds obtained with our method, in modular arithmetic (\({{\mathbb{Z}}}_{2}\)) and standard arithmetic.

In all cases, AlphaTensor discovers algorithms that match or improve over known state of the art (improvements are shown in red).

1 and 2 for examples of algorithms found with AlphaTensor.

Right: results (for arithmetic in \({\mathbb{R}}\)) of applying AlphaTensor-discovered algorithms on larger tensors.

AlphaTensor generates a large database of matrix multiplication algorithms—up to thousands of algorithms for each size.

We exploit this rich space of algorithms by combining them recursively, with the aim of decomposing larger matrix multiplication tensors.

Using this approach, we improve over the state-of-the-art results for more than 70 matrix multiplication tensors (with n, m, p ≤ 12).

By training one agent to decompose various tensors, AlphaTensor shares learned strategies among these, thereby improving the overall performance (see Supplementary Information for analysis).

Finally, it is noted that AlphaTensor scales beyond current computational approaches for decomposing tensors.

From a mathematical standpoint, the diverse algorithms discovered by AlphaTensor show that the space is richer than previously known.

For example, while the only known rank-49 factorization decomposing \({{\mathscr{T}}}_{4}={{\mathscr{T}}}_{2}\otimes {{\mathscr{T}}}_{2}\) before this paper conforms to the product structure (that is, it uses the factorization of \({{\mathscr{T}}}_{2}\) twice, which we refer to as Strassen-square2), AlphaTensor finds more than 14,000 non-equivalent factorizations (with standard arithmetic) that depart from this scheme, and have different properties (such as matrix ranks and sparsity—see Supplementary Information).

Such properties of matrix multiplication tensors are of great interest, as these tensors represent fundamental objects in algebraic complexity theory3,5,7.

The study of matrix multiplication symmetries can also provide insight into the asymptotic complexity of matrix multiplication5.

By exploring this rich space of algorithms, we believe that AlphaTensor will be useful for generating results and guiding mathematical research.

Tensors can represent any bilinear operation, such as structured matrix multiplication, polynomial multiplication or more custom bilinear operations used in machine learning27,28.

We demonstrate here a use-case where AlphaTensor finds a state-of-the-art algorithm for multiplying an n x n skew-symmetric matrix  with a vector of length n.

This algorithm, which uses \((n-1)(n+2)/2 \sim \frac{1}{2}{n}^{2}\) multiplications (where ∼ indicates asymptotic similarity), outperforms the previously known algorithms using asymptotically n2 multiplications29, and is asymptotically optimal.

This shows that AlphaTensor can be applied to custom bilinear operations, and yield efficient algorithms leveraging the problem structure.

a, Decompositions found by AlphaTensor for the tensors of size \(\frac{n(n-1)}{2}\times n\times n\) (with n = 3, 4, 5, 6) representing the skew-symmetric matrix-vector multiplication.

b, Skew-symmetric matrix-by-vector multiplication algorithm, obtained from the examples solved by AlphaTensor.

We show a use-case where AlphaTensor finds practically efficient matrix multiplication algorithms, tailored to specific hardware, with zero prior hardware knowledge.

To do so, we modify the reward of AlphaTensor: we provide an additional reward at the terminal state (after the agent found a correct algorithm) equal to the negative of the runtime of the algorithm when benchmarked on the target hardware.

We train AlphaTensor to search for efficient algorithms to multiply 4 × 4 block matrices, and focus on square matrix multiplication of size 8,192 (each block is hence of size 2,048) to define the benchmarking reward.

We do not apply the 4 × 4 algorithm recursively, to leverage the efficient implementation of matrix multiplication on moderate-size matrices (2,048 × 2,048 in this case).

The factorization obtained by AlphaTensor is transformed into JAX30 code, which is compiled (just in time) before benchmarking.

AlphaTensor discovers algorithms that outperform the Strassen-square algorithm, which is a fast algorithm for large square matrices31,32.

Although the discovered algorithm has the same theoretical complexity as Strassen-square, it outperforms it in practice, as it is optimized for the considered hardware.

Interestingly, AlphaTensor finds algorithms with a larger number of additions compared with Strassen-square (or equivalently, denser decompositions), but the discovered algorithms generate individual operations that can be efficiently fused by the specific XLA33 grouping procedure and thus are more tailored towards the compiler stack we use.

The algorithms found by AlphaTensor also provide gains on matrix sizes larger than what they were optimized for.

a,b, Speed-ups (%) of the AlphaTensor-discovered algorithms tailored for a GPU (a) and a TPU (b), optimized for a matrix multiplication of size 8,192 × 8,192.

Speed-ups are measured relative to standard (for example, cuBLAS for the GPU) matrix multiplication on the same hardware.

Speed-ups are reported for various matrix sizes (despite optimizing the algorithm only on one matrix size).

Trained from scratch, AlphaTensor discovers matrix multiplication algorithms that are more efficient than existing human and computer-designed algorithms.

Despite improving over known algorithms, we note that a limitation of AlphaTensor is the need to pre-define a set of potential factor entries F, which discretizes the search space but can possibly lead to missing out on efficient algorithms.

An interesting direction for future research is to adapt AlphaTensor to search for F.

One important strength of AlphaTensor is its flexibility to support complex stochastic and non-differentiable rewards (from the tensor rank to practical efficiency on specific hardware), in addition to finding algorithms for custom operations in a wide variety of spaces (such as finite fields).

We believe this will spur applications of AlphaTensor towards designing algorithms that optimize metrics that we did not consider here, such as numerical stability or energy usage.

The discovery of matrix multiplication algorithms has far-reaching implications, as matrix multiplication sits at the core of many computational tasks, such as matrix inversion, computing the determinant and solving linear systems, to name a few7.

We also note that our methodology can be extended to tackle related primitive mathematical problems, such as computing other notions of rank (for example, border rank—see Supplementary Information), and NP-hard matrix factorization problems (for example, non-negative factorization).

The game ends when the state reaches the zero tensor, \({{\mathscr{S}}}_{R}={\bf{0}}\).

This means that the factors written down throughout the game form a factorization of the start tensor \({{\mathscr{S}}}_{0}\), that is, \({{\mathscr{S}}}_{0}={\sum }_{t=1}^{R}{{\bf{u}}}^{(t)}\otimes {{\bf{v}}}^{(t)}\otimes {{\bf{w}}}^{(t)}\).

For example, when optimizing for asymptotic time complexity, this penalty is derived from an upper bound on the tensor rank of the final residual tensor \({{\mathscr{S}}}_{{R}_{\text{limit}}}\).

This upper bound on the tensor rank is obtained by summing the matrix ranks of the slices of the tensor.

The tensor rank depends, in general, on the ring.

The parameters θ of the deep neural network are trained by reinforcement learning from self-play games and synthetic demonstrations.

The distribution over returns z(⋅∣st) is learned through distributional reinforcement learning using the quantile regression distributional loss34, and the network policy π(⋅∣st) is updated using a Kullback–Leibler divergence loss, to maximize its similarity to the search policy for self-play games or to the next action for synthetic demonstrations.

In addition, a transposition table is used to recombine different action sequences if they reach the exact same tensor.

Differently from AlphaZero and Sampled AlphaZero, we chose v not to be the mean of the distribution of returns z(⋅∣sL) as is usual in most reinforcement learning agents, but instead to be a risk-seeking value, leveraging the facts that TensorGame is a deterministic environment and that we are primarily interested in finding the best trajectory possible.

We train a single agent to decompose the different tensors \({{\mathscr{T}}}_{n,m,p}\) in a given arithmetic (standard or modular).

As the network works with fixed-size inputs, we pad all tensors (with zeros) to the size of the largest tensor we consider (\({{\mathscr{T}}}_{5}\), of size 25 × 25 × 25).

Owing to learned transfer between the two arithmetics, this agent discovers a different distribution of algorithms (of the same ranks) in standard arithmetic than the agent trained on standard arithmetic only, thereby increasing the overall diversity of discovered algorithms.

The synthetic demonstrations buffer contains tensor-factorization pairs, where the factorizations \({\{({{\bf{u}}}^{(r)},{{\bf{v}}}^{(r)},{{\bf{w}}}^{(r)})\}}_{r=1}^{R}\) are first generated at random, after which the tensor \({\mathscr{D}}={\sum }_{r=1}^{R}{{\bf{u}}}^{(r)}\otimes {{\bf{v}}}^{(r)}\otimes {{\bf{w}}}^{(r)}\) is formed.

The rank of a bilinear operation does not depend on the basis in which the tensor representing it is expressed, and for any invertible matrices A, B and C we have \({\rm{Rank}}\,({\mathscr{T}})={\rm{Rank}}\,({{\mathscr{T}}}^{({\bf{A}},{\bf{B}},{\bf{C}})})\), where \({{\mathscr{T}}}^{({\bf{A}},{\bf{B}},{\bf{C}})}\) is the tensor after change of basis given by.

Hence, exhibiting a rank-R decomposition of the matrix multiplication tensor \({{\mathscr{T}}}_{n}\) expressed in any basis proves that the product of two n × n matrices can be computed using R scalar multiplications.

We leverage this observation by expressing the matrix multiplication tensor \({{\mathscr{T}}}_{n}\) in a large number of randomly generated bases (typically 100,000) in addition to the canonical basis, and letting AlphaTensor play games in all bases in parallel.

This approach has three appealing properties: (1) it provides a natural exploration mechanism as playing games in different bases automatically injects diversity into the games played by the agent; (2) it exploits properties of the problem as the agent need not succeed in all bases—it is sufficient to find a low-rank decomposition in any of the bases; (3) it enlarges coverage of the algorithm space because a decomposition with entries in a finite set F = {−2, −1, 0, 1, 2} found in a different basis need not have entries in the same set when converted back into the canonical basis.

In full generality, a basis change for a 3D tensor of size S × S × S is specified by three invertible S × S matrices A, B and C.

At acting time, when the network is queried, we transform the input tensor by applying a change of basis—where the change of basis matrix is set to a random signed permutation.

We then query the network on this transformed input tensor, and finally invert the transformation in the network’s policy predictions.

For any λ1, λ2, λ3 ∈ {−1, +1} such that λ1λ2λ3 = 1, the actions (λ1u, λ2v, λ3w) and (u, v, w) are equivalent because they lead to the same rank-one tensor (λ1u) ⊗ (λ2v) ⊗ (λ3w) = u ⊗ v ⊗ w.

This is well defined because u or v cannot be all zeros (if they are to be part of a minimal rank decomposition), and for any (u, v, w) there are unique λ1, λ2, λ3 ∈ {−1, +1} (with λ1λ2λ3 = 1) that transform it into canonical form.

The most important piece of information is the current 3D tensor \({{\mathscr{S}}}_{t}\) of size S × S × S.

(For simplicity, in the description here we assume that all the three dimensions of the tensor are equal in size. The generalization to different sizes is straightforward.) In addition, the model is given access to the last h actions (h being a hyperparameter usually set to 7), represented as h rank-1 tensors that are concatenated to the input.

Each grid represents two out of the three modes of the tensor.

Defining the modes of the tensor as \({\mathcal{U}},{\mathcal{V}},{\mathcal{W}}\), the rows and columns of the first grid are associated to \({\mathcal{U}}\) and \({\mathcal{V}}\), respectively, the rows and columns of the second grid are associated to \({\mathcal{W}}\) and \({\mathcal{U}}\), and the rows and columns of the third grid are associated to \({\mathcal{V}}\) and \({\mathcal{W}}\).

The quest for efficient matrix multiplication algorithms started with Strassen’s breakthrough in ref.

This led to the development of a very active field of mathematics attracting worldwide interest, which studies the asymptotic complexity of matrix multiplication (see refs. 3,4,5,6).

So far, the best known complexity for matrix multiplication is \({\mathcal{O}}({n}^{2.37286})\) (ref. 12), which improves over ref.

However, this does not yield practical algorithms, as such approaches become advantageous only for astronomical matrix sizes.

Hence, a significant body of work aims at exhibiting explicit factorizations of matrix multiplication tensors, as these factorizations provide practical algorithms.

After Strassen’s breakthrough showing that \(\text{rank}\,({{\mathscr{T}}}_{2})\le 7\), efficient algorithms for larger matrix sizes were found15,16,18,26,38.

In addition to providing individual low-rank factorizations, an important research direction aims at understanding the space of matrix multiplication algorithms—as opposed to exhibiting individual low-rank factorizations—by studying the symmetry groups and diversity of factorizations (see ref. 5 and references therein).

For example, the symmetries of 2 × 2 matrix multiplication were studied in refs.

On the computational front, continuous optimization has been the main workhorse for decomposing tensors17,45,46, and in particular matrix multiplication tensors.

Such continuous optimization procedures (for example, alternating least squares), however, yield approximate solutions, which correspond to inexact matrix multiplication algorithms with floating point operations.

47,48, based on learning the continuous weights of a two-layer network that mimics the structure of the matrix multiplication operation.

This method, which is trained through supervised learning of matrix multiplication examples, finds approximate solutions to 2 × 2 and 3 × 3 matrix multiplications.

Unlike continuous optimization-based approaches, AlphaTensor directly produces algorithms from the desired set of valid algorithms, and is flexible in that it allows us to optimize a wide range of (even non-differentiable) objectives.

Different from continuous optimization, a boolean satisfiability (SAT) based  formulation of the problem of decomposing 3 × 3 matrix multiplication was recently proposed in ref.

20, which adds thousands of new decompositions of rank 23 to the list of known 3 × 3 factorizations.

As is, this approach is, however, unlikely to scale to larger tensors, as the search space grows very quickly with the size.

31 proposed several ideas to speed up implementation of fast matrix multiplication algorithms on central processing units (CPUs).

Different fast algorithms are then compared and benchmarked, and the potential speed-up of such algorithms is shown against standard multiplication.

Other works focused on getting the maximal performance out of a particular fast matrix multiplication algorithm (Strassen’s algorithm with one or two levels of recursion) on a CPU32 or a GPU49.

We see writing a custom low-level implementation of a given algorithm to be distinct from the focus of this paper—developing new efficient algorithms—and we believe that the algorithms we discovered can further benefit from a more efficient implementation by experts.

Beyond matrix multiplication and bilinear operations, a growing amount of research studies the use of optimization and machine learning to improve the efficiency of computational operations.

Our work focuses on the algorithmic level of abstraction, although AlphaTensor is also flexible to discover efficient algorithms for specific hardware.

Different from previous works, we focus on discovering matrix multiplication algorithms that are provably correct, without requiring initial reference implementations.

We conclude by relating our work broadly to existing reinforcement learning methods for scientific discovery.

Within mathematics, reinforcement learning was applied, for example, to theorem proving55,56,57,58, and to finding counterexamples refuting conjectures in combinatorics and graph theory59.

The algorithms discovered by AlphaTensor are available for download at https://github.com/deepmind/alphatensor.

A general reinforcement learning algorithm that masters chess, shogi, and Go through self-play.

Fast matrix multiplication.

Fast feasible and unfeasible matrix multiplication.

Partial and total matrix multiplicationJ

Matrix multiplication via arithmetic progressions.

The asymptotic spectrum of tensors and the exponent of matrix multiplication.

Powers of tensors and fast matrix multiplication.

A refined laser method and faster matrix multiplication.

Most tensor problems are NP-hard.

On minimizing the number of multiplications necessary for matrix multiplication.

The bilinear complexity and practical algorithms for matrix multiplication.

The tensor rank of 5x5 matrices multiplication is bounded by 98 and its border rank by 89.

Optimization techniques for small matrix multiplication.

Fast structured matrix computations: tensor rank and Cohn–Umans methodM

A framework for practical parallel fast matrix multiplication.

optimal algorithms for 2 × 2-matrix multiplication.

The geometry of rank decompositions of matrix multiplication I: 2 × 2 matrices.

The geometry of rank decompositions of matrix multiplication II: 3 × 3 matrices.

Matrix multiplication algorithms from group orbits.

Tensor decompositions and applications.

General tensor decomposition, moment matrices and applications.

Algorithm selection using reinforcement learning.

Optimization of molecules via deep reinforcement learning.

Fast matrix multiplication algorithms catalogue.

developed the tensor decomposition environment and data generation pipeline, and A.H., T.H., M.

analysed the experimental results and algorithms discovered by AlphaTensor.

Discovering faster matrix multiplication algorithms with reinforcement learning